Revisiting Division: Understanding Different Interpretations
Written on
Chapter 1: The Dual Nature of Division
Division can often be misunderstood. The way we interpret division can lead to two conflicting viewpoints, suggesting that distinct operations warrant unique symbols.
Is there a significant distinction between three couples and two throuples? Absolutely! While both configurations include six individuals in total, how these six are organized into equally sized groups is crucial.

The expression “3 × 2” yields different real-world implications based on its interpretation. For instance, in the first scenario, we can visualize six individuals arranged into three couples, a socially accepted division. In contrast, the second scenario involves two throuples (or ménages à trois), a more unconventional romantic arrangement.
This example clearly illustrates that in human relationships, 3 × 2 does not equal 2 × 3. But what does this have to do with division?
When asked to organize six individuals into three couples instead of two throuples, how would you mathematically represent this? Would it be written as: 6 ÷ 2 = 3? What practical outcome does this lead to? Does it create two groups of three, or three groups of two?

The equation “6 ÷ 2 = 3” can be interpreted in two ways: it might represent either three groups of two individuals or two groups of three individuals.
You might exclaim, “Oh no, ‘6 ÷ 2 = 3’ is unclear!” But consider the case of 6 ÷ 3 = 2 as a precise mathematical expression for dividing six individuals into three couples.

Once again, “6 ÷ 3 = 2” presents two interpretations: either three groups of two individuals or two groups of three individuals. This ambiguity arises from the commutative property of multiplication, where 3 × 2 = 6 = 2 × 3. Essentially, there are two distinct arrangements of equally-sized groups that total six individuals, and our existing notation fails to differentiate between them.
Section 1.1: The Case for Distinct Symbols
Different operations necessitate unique symbols: “+” should represent “addition,” not “addition or subtraction depending on the author's intent.” The obelus symbol, ÷, is employed in English-speaking regions to denote two variations of division: partitive and quotitive.
How are these two forms symbolically represented? Unfortunately, they aren't.
In a typical division problem, we deal with three numbers: the dividend (the number to be divided), the divisor (the number by which we divide), and the quotient (the result of the division).

If you determine that the number of equally-sized groups should match the divisor, you are performing partitive division.

Conversely, if you decide that the number of equally-sized groups should correspond to the quotient, you are conducting quotitive division. This type of division involves repeatedly subtracting the divisor from the dividend and counting the resulting groups.
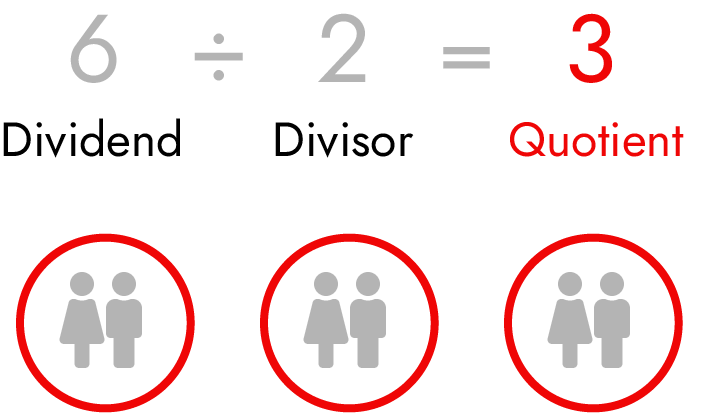
The inherent ambiguity in symbolic representation is problematic, but I propose a solution.
Section 1.2: Proposing a New Symbol for Partitive Division
Interestingly, the obelus symbol, ÷, has been historically used to signify subtraction in various regions, such as Norway and Denmark. Given its appearance—similar to the subtraction symbol, ?—with an additional couple of dots, I propose retaining it for quotitive division, meaning “Take the divisor from the dividend until nothing remains.” Thus, 6 ÷ 2 = 3 would indicate “Subtract two from six until you can no longer subtract,” resulting in three groups of two.
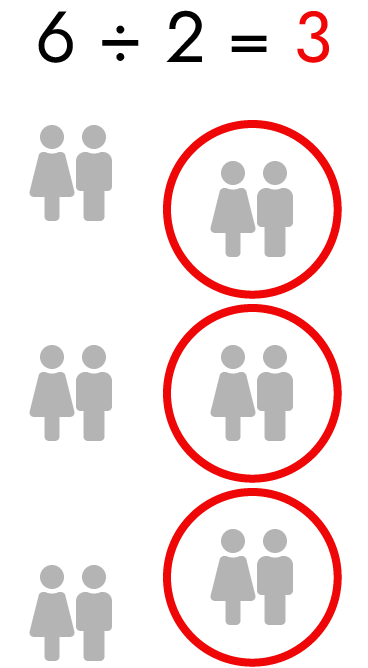
For partitive division, I suggest a new symbol: a right-turned capital Latin “Y,” which would effectively communicate the idea of dividing the dividend into a set number of equally-sized groups, where the number of these groups corresponds to the divisor.
Unfortunately, a right-turned capital Latin “Y” does not exist in Unicode, prompting me to devise a makeshift representation for this article: -<.

So, 6 -< 2 = 3 would signify “Divide six into two equal groups,” yielding two groups of three.

While I explored various other Unicode symbols, such as ? (a turned sans-serif capital Latin “Y”), I found they failed to convey the concept of “dividing into equally-sized groups” as effectively as the proposed right-turned “Y.”
What are the next steps?
The primary challenges facing my proposal include a lack of interest from the mathematical, educational, and general communities, as well as the absence of Unicode support for a new right-turned “Y.”
I welcome your thoughts on this proposal in the comments. Did it shed light on any confusion you had regarding division? Or do you consider this idea unnecessary and unwarranted? Meanwhile, I may begin advocating with the Unicode working group.
Chapter 2: Practical Approaches to Division
Explore effective strategies for teaching division to elementary students, including visual aids and engaging methods.
Learn how to quickly perform mental calculations for division, suitable for beginners looking to sharpen their math skills.